
Practically, such a matrix is almost singular, and the computation of its inverse, or solution of a linear system of equations is prone to large numerical errors. If the condition number is very large, then the matrix is said to be ill-conditioned. If the condition number is not significantly larger than one, the matrix is well-conditioned, which means that its inverse can be computed with good accuracy. The condition number computed with this norm is generally larger than the condition number computed relative to the Euclidean norm, but it can be evaluated more easily (and this is often the only practicably computable condition number, when the problem to solve involves a non-linear algebra, for example when approximating irrational and transcendental functions or numbers with numerical methods). Recalling that the eigenvalues of any triangular matrix are simply the diagonal entries. an integer or numeric matrix of the same dimensions as frame. Very frequently, one is solving the inverse problem: given f ( x ) = y, Return the matrix obtained by converting all the variables in a data frame to numeric mode. This is used to measure how sensitive a function is to changes or errors in the input, and how much error in the output results from an error in the input. Future Raspbian images will ship with the Wolfram Language and Mathematica by default existing users with at least 600MB of free space on their SD card can install them today by typing: sudo apt-get update & sudo apt-get install wolfram-engine You’ll find Mathematica in the app launcher under the Education menu.
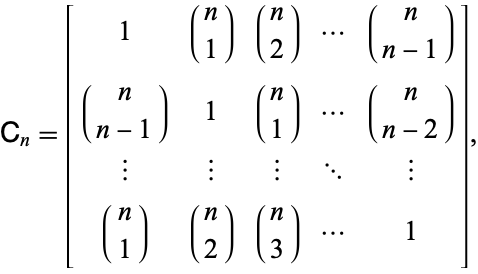
In numerical analysis, the condition number of a function measures how much the output value of the function can change for a small change in the input argument. Measure of a function's sensitivity to input change or error


 0 kommentar(er)
0 kommentar(er)
